Those Greeks were smart cookies.

I don't think we appreciate a man known for a theorem nearly enough.  Pythagoras was one awesome dude.  

I think most of us remember, a^2 + b^2 = c^2. 

But do we really understand just how useful that theorem is, and how it can be used?  

Or how about Euclid?  For instance we 

know all about parallel lines, but, man.. do we really understand why and how the concept of a straight line, rays, angles and parallel lines is just.. cool?

Since relearning geometry, i have started to really been blown away by just how significant, euclid and pythagoras were.

It seems like a weird thing to think about parallel lines as being important, but once you put a line through those parallel lines all sorts of possibilities are learned.

For those who may have forgotten, here are some euclidean axioms.

a) any two points can be joined by a line segment

b) any line segment can be extended to a line.  

c) Given any point P and any length r, there is a circle of radius r with P at its center.

d) Any two right angles are congruent.

e)If a straight line N intersects two straight lin

es L and M, and if the interior angles on one side of N add up to less than two right angles, then the lines L and M intersect on that side of N.   This 5th axiom is also known as the parallel postulate or, for every line Y, and a point X not on the line, there is one and only one line that contains point X and is parallel to Y.  

It is amazing that these 5 axioms built the entire field of euclidean geometry.  

For instance, do you want to prove that a triangle has 180 degrees?  All we need is to accept that right angle has 90 degrees and we are well on our way.

So let's look at this di

agram from here on out.  

What do we need to know...

Using euclid's axioms we need to prove that angle a up top is = to angle a inside the

 triangle.  Same with angles b. 

Once we get there, it becomes easy, since we know that angles a + b + c = 180 degrees since they make up a single straight line.  (remember once we accept a right angle as 90 degrees a straight line clearly is 180 degrees simply by placeing them next to each other).  

So how do we prove that angle a is the same in the triangle and next to the straight line? 

We use the last axiom.... here is how the last axiom looks...

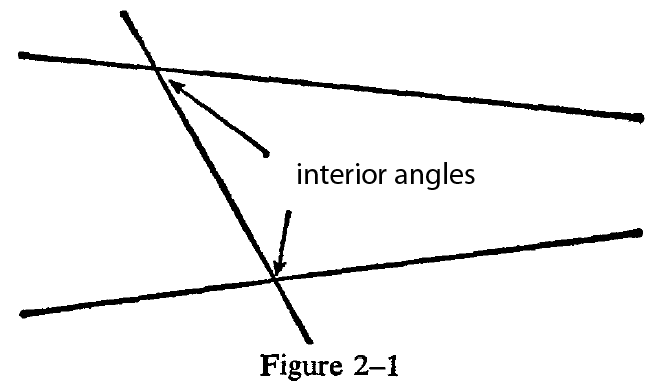
Essentially we take corrollary of this axiom.  Essentially if the 2 lines do not meet, then it means the interior angles must be AT LEAST = 180 degrees.  If they are less, than by definition they would meet on that side of the intersecting line.  

So instead of using 2 random lines, we use parallel lines and a single intersecting line.  We know that the interior angles would have to total at least 180 degrees.  

What this means so far is that angles B + C and G + F  must be at least 180 degrees.  Since we know that a = straight line (by definition) = 180 degrees, then angles B + G = 180, and C + F = 180. So now we use some algebra...

F + C = 180 which means F = 180 - C.  This means that G + (180 -C) must be at least = to 180.   This would translate to G -C >0.  This means G must be at least = C.  

Now, using the other way G + B = 180, Which means B = 180-G. and since B + C must be at least 180, this means that 180-G + C  must be equal or greater than 180. Essentially this will mean that C - G > = 0 now for  G- C >= 0 and C-G >= 0, then G must be equal to C.

Once we get to G = C, then F = B, and we suddenly have opposite angles on parallel angles being =. And we can use this result to show that the angles a in the first triangle are = and that gets us to the fact that a triangle has 180 degrees. 

This fascinating to me.  When we say a triangle has 180 degrees what we are really saying is that a triangle has the same number of degrees as what we assign to a straight line, or double what we assign to a right angle.  Remember the numbers are completely arbitrary.  I could just as easily claim that a straight line has 10 "degrees", this is just nomenclature. But if i did claim that a straight line has 10 degrees, i would be forced to also claim that a triangle has 10 "degree" and a right angle has 5 "degrees".  That is amazing, since we are forced to agree accept that a triangle has the same number of degrees as a straight line no matter, what we assign to the straight line. 

It is through those simple set of axioms and nomenclature that we can use to build up the entire discipline. 

Neat-O stuff!