Wednesday, October 15, 2008
Sorry!
For the lack of updates. I just don't have much to say, trying to keep up the studying. I should have something for y'all soon!
Monday, October 6, 2008
Os, Radii, PIE!!

If you pay any attention to baseball, you will know that I, sadly, will have no excuse for being distracted by Cubs baseball. After what could only be described as putrid performances, I have no excuse to stray from my studies.
A couple of hurdles...
1) Sleep. I don't get enough of it. I usually go to bed between 1:30 and 2 am, which means i average about 5 1/2 hours of sleep. This has actually been a decent amount for me, as i have been known to subsist on 4 hours a night. However, this does mean that as i get home after 7 pm, with the skies dark, i am SLEEPY. It is hard to focus, and my last instinct is to grab the books and try and wrestle with proofs, theorems and axioms. I have absolutely new found respect to those who go to school and work at the same time.
2) Food. I have been relatively good about not relying
on restuarants or pre-made meals for dinner. But, this means i usually have to think, plan and sometimes even (shockingly) cook. This means that i am unable to split my concentration for studying and i end up lying happily on my couch sated, and much more inclined to nap than hitting the books.
So.. a special shout-out to student-mothers!!
I am on Circles, which for the most part hasn't been difficult in one sense. Pi r Squared = Area and 2r PI = Circumference is pretty much what elementary geometry cares about.
But, and this is has always been a bit of struggle, the more i think about Pi, the more fascinating it really is.
Below is the simple image:
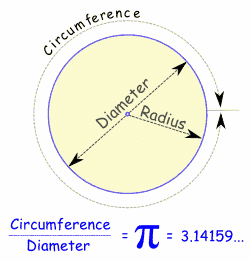
Of course, my book, in order to get you working on problems, likes to say, Pi can be generally expressed as 22/7.. which is silly. We all know that Pi is this super irrational number, and one that people obssess over.
I always found it interesting that one measure of geekiness and nerd-fu, was to see how many digits of Pi one has memorized. From what i know, there are still scientists and computer programmers trying to figure out how many digits they can get to.
There is no such parallel obsession with e, or Euler's number, or even the golden ratio, both of which are irrational numbers.
One reason, i think pi has been such a folktale, has been that it SEEMS like something we could see, and even measure.
For instance, let's say i take a normal compass, and draw a circle on a piece of paper with a radius of 1/2 cm. Well by definition we know that 2rPi = Circumference. This means that the circumference of my circle should be exactly Pi centimeters. Easy right? But, of course if i measure the actual circumference with a piece of twine or what not, i'll probably come up with some variation of 3.1 cm. It wouldn't matter how accurate i have of a compass, or that i could use a single micron to draw the circle, or be able to measure to an angstrom the total circumference of the circle; i would never be able to get the circumference to measure and equal Pi. Instead, i'll just get closer and closer. That is sort of weird isn't it? I mean, not only is the concept of the number hard to get my mind around, but how in the world did they even realize that no matter how precise the measurement, it would never be "accurate."
The other way to think about Pi is that because it is expressed as a ratio, it is NOT contingent on forms of measurement.. For instance, we are taught in school that a circle has 360 degrees. But of course a "degree" is just a form of measurement that we create in order to understand circles and geometric shape. We could just as easily say that a circle has 200 degrees and we wouldn't be inaccurate, we would just define degrees differently. Of course no matter what, we can't change the ration between a radius of a circle and its area or circumference.
For instance, why do we think that a circle has 360 degrees? Because we have based degrees or "radians" on PI itself. A radian is defined as a unit of measure a "central angle" of a circle, if the arc of the central angle is equal to the radius of the central angle. This is used to show that a PI is by definition 180 degrees, since the circumference of a circle with radius 1 is 2PI, and therefore 1/2 a circle is 180 degrees (and thus Pi). Weird? Well sure, it is all because we base everything on the ratio that we don't have any control over.
Thursday, October 2, 2008
Distraction!
Subscribe to:
Posts (Atom)

