Wednesday, October 15, 2008
Sorry!
For the lack of updates. I just don't have much to say, trying to keep up the studying. I should have something for y'all soon!
Monday, October 6, 2008
Os, Radii, PIE!!

If you pay any attention to baseball, you will know that I, sadly, will have no excuse for being distracted by Cubs baseball. After what could only be described as putrid performances, I have no excuse to stray from my studies.
A couple of hurdles...
1) Sleep. I don't get enough of it. I usually go to bed between 1:30 and 2 am, which means i average about 5 1/2 hours of sleep. This has actually been a decent amount for me, as i have been known to subsist on 4 hours a night. However, this does mean that as i get home after 7 pm, with the skies dark, i am SLEEPY. It is hard to focus, and my last instinct is to grab the books and try and wrestle with proofs, theorems and axioms. I have absolutely new found respect to those who go to school and work at the same time.
2) Food. I have been relatively good about not relying
on restuarants or pre-made meals for dinner. But, this means i usually have to think, plan and sometimes even (shockingly) cook. This means that i am unable to split my concentration for studying and i end up lying happily on my couch sated, and much more inclined to nap than hitting the books.
So.. a special shout-out to student-mothers!!
I am on Circles, which for the most part hasn't been difficult in one sense. Pi r Squared = Area and 2r PI = Circumference is pretty much what elementary geometry cares about.
But, and this is has always been a bit of struggle, the more i think about Pi, the more fascinating it really is.
Below is the simple image:
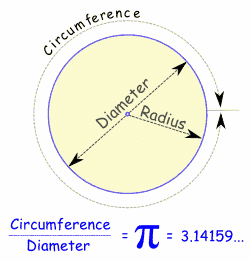
Of course, my book, in order to get you working on problems, likes to say, Pi can be generally expressed as 22/7.. which is silly. We all know that Pi is this super irrational number, and one that people obssess over.
I always found it interesting that one measure of geekiness and nerd-fu, was to see how many digits of Pi one has memorized. From what i know, there are still scientists and computer programmers trying to figure out how many digits they can get to.
There is no such parallel obsession with e, or Euler's number, or even the golden ratio, both of which are irrational numbers.
One reason, i think pi has been such a folktale, has been that it SEEMS like something we could see, and even measure.
For instance, let's say i take a normal compass, and draw a circle on a piece of paper with a radius of 1/2 cm. Well by definition we know that 2rPi = Circumference. This means that the circumference of my circle should be exactly Pi centimeters. Easy right? But, of course if i measure the actual circumference with a piece of twine or what not, i'll probably come up with some variation of 3.1 cm. It wouldn't matter how accurate i have of a compass, or that i could use a single micron to draw the circle, or be able to measure to an angstrom the total circumference of the circle; i would never be able to get the circumference to measure and equal Pi. Instead, i'll just get closer and closer. That is sort of weird isn't it? I mean, not only is the concept of the number hard to get my mind around, but how in the world did they even realize that no matter how precise the measurement, it would never be "accurate."
The other way to think about Pi is that because it is expressed as a ratio, it is NOT contingent on forms of measurement.. For instance, we are taught in school that a circle has 360 degrees. But of course a "degree" is just a form of measurement that we create in order to understand circles and geometric shape. We could just as easily say that a circle has 200 degrees and we wouldn't be inaccurate, we would just define degrees differently. Of course no matter what, we can't change the ration between a radius of a circle and its area or circumference.
For instance, why do we think that a circle has 360 degrees? Because we have based degrees or "radians" on PI itself. A radian is defined as a unit of measure a "central angle" of a circle, if the arc of the central angle is equal to the radius of the central angle. This is used to show that a PI is by definition 180 degrees, since the circumference of a circle with radius 1 is 2PI, and therefore 1/2 a circle is 180 degrees (and thus Pi). Weird? Well sure, it is all because we base everything on the ratio that we don't have any control over.
Thursday, October 2, 2008
Distraction!
Tuesday, September 30, 2008
Those Greeks were smart cookies.

I don't think we appreciate a man known for a theorem nearly enough. Pythagoras was one awesome dude.
I think most of us remember, a^2 + b^2 = c^2.
But do we really understand just how useful that theorem is, and how it can be used?
Or how about Euclid? For instance we
know all about parallel lines, but, man.. do we really understand why and how the concept of a straight line, rays, angles and parallel lines is just.. cool?
Since relearning geometry, i have started to really been blown away by just how significant, euclid and pythagoras were.
It seems like a weird thing to think about parallel lines as being important, but once you put a line through those parallel lines all sorts of possibilities are learned.
For those who may have forgotten, here are some euclidean axioms.
a) any two points can be joined by a line segment
b) any line segment can be extended to a line.
c) Given any point P and any length r, there is a circle of radius r with P at its center.
d) Any two right angles are congruent.
e)If a straight line N intersects two straight lin
es L and M, and if the interior angles on one side of N add up to less than two right angles, then the lines L and M intersect on that side of N. This 5th axiom is also known as the parallel postulate or, for every line Y, and a point X not on the line, there is one and only one line that contains point X and is parallel to Y.
It is amazing that these 5 axioms built the entire field of euclidean geometry.
For instance, do you want to prove that a triangle has 180 degrees? All we need is to accept that right angle has 90 degrees and we are well on our way.

So let's look at this di
agram from here on out.
What do we need to know...
Using euclid's axioms we need to prove that angle a up top is = to angle a inside the
triangle. Same with angles b.
Once we get there, it becomes easy, since we know that angles a + b + c = 180 degrees since they make up a single straight line. (remember once we accept a right angle as 90 degrees a straight line clearly is 180 degrees simply by placeing them next to each other).
So how do we prove that angle a is the same in the triangle and next to the straight line?
We use the last axiom.... here is how the last axiom looks...
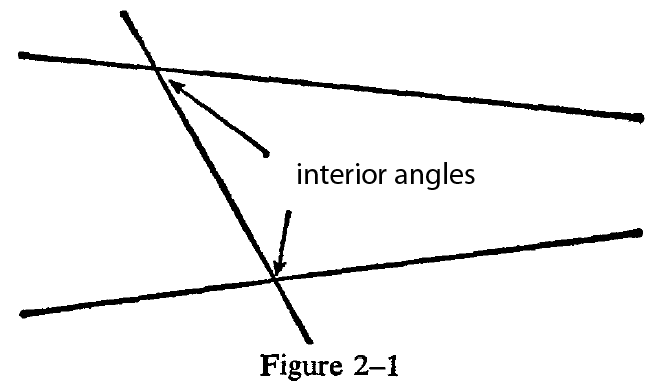
Essentially we take corrollary of this axiom. Essentially if the 2 lines do not meet, then it means the interior angles must be AT LEAST = 180 degrees. If they are less, than by definition they would meet on that side of the intersecting line.
So instead of using 2 random lines, we use parallel lines and a single intersecting line. We know that the interior angles would have to total at least 180 degrees.

What this means so far is that angles B + C and G + F must be at least 180 degrees. Since we know that a = straight line (by definition) = 180 degrees, then angles B + G = 180, and C + F = 180. So now we use some algebra...
F + C = 180 which means F = 180 - C. This means that G + (180 -C) must be at least = to 180. This would translate to G -C >0. This means G must be at least = C.
Now, using the other way G + B = 180, Which means B = 180-G. and since B + C must be at least 180, this means that 180-G + C must be equal or greater than 180. Essentially this will mean that C - G > = 0 now for G- C >= 0 and C-G >= 0, then G must be equal to C.
Once we get to G = C, then F = B, and we suddenly have opposite angles on parallel angles being =. And we can use this result to show that the angles a in the first triangle are = and that gets us to the fact that a triangle has 180 degrees.
This fascinating to me. When we say a triangle has 180 degrees what we are really saying is that a triangle has the same number of degrees as what we assign to a straight line, or double what we assign to a right angle. Remember the numbers are completely arbitrary. I could just as easily claim that a straight line has 10 "degrees", this is just nomenclature. But if i did claim that a straight line has 10 degrees, i would be forced to also claim that a triangle has 10 "degree" and a right angle has 5 "degrees". That is amazing, since we are forced to agree accept that a triangle has the same number of degrees as a straight line no matter, what we assign to the straight line.
It is through those simple set of axioms and nomenclature that we can use to build up the entire discipline.
Neat-O stuff!
Saturday, September 27, 2008
Thanks Andrew Carnagie!
 I went hunting for textbooks in math, especially geometry and trigonometry. As I mentioned in my prior post, i wanted to try Powell's. (i went to the one in Lincoln avenue instead of hyde park at first.) The bookstore was pretty great, but, sadly, no real textbooks. There were rows and rows of reporters from various math conferences. There were a few interesting books on advanced numbers theory, topology and crytography, but sadly, nothing at my level. I did find a cheap used copy of "Everything and more" by DFW, but while i think that would be fun to read, it doesn't quite get me there.
I went hunting for textbooks in math, especially geometry and trigonometry. As I mentioned in my prior post, i wanted to try Powell's. (i went to the one in Lincoln avenue instead of hyde park at first.) The bookstore was pretty great, but, sadly, no real textbooks. There were rows and rows of reporters from various math conferences. There were a few interesting books on advanced numbers theory, topology and crytography, but sadly, nothing at my level. I did find a cheap used copy of "Everything and more" by DFW, but while i think that would be fun to read, it doesn't quite get me there. As I was trying to figure out whether to make the trip all the way to Hyde Park, I had a sudden moment of inspiration. What if the citizens of my fair city had already provided the resources to get me to my goal?
One of the coolest perks of large cities like Chicago, are the well stocked nature and availability of public libraries. And right near my apartment, across from a bar, down a block from a 7-Eleven and a liquor store, is a nice institution of learning and community. It took me less than 3 minutes to find a coupl of textbooks on Geometry, including a book that was from the "Self-teaching guide" series... apparently i am not the only one with this idea.
Tuesday, September 23, 2008
Abstract Understanding

I haven't been able to really jump in and start to study geometry and trigonometry yet, as i haven't been able to find a good textbook. I went to my university's (i am a staff attorney at a local university's legal clinic) bookstore, and looked for a textbook. Sadly, I could only find a single textbook on math, and it was a "pre-calculus" textbook. It just didn't feel like it was what i was looking for.


I think the best plan would be to go to the used bookstores near universities (there is a great Powell's near the UofC) and look for some text books there. (Yeah yeah, any excuse to go to a used bookstore!).

But fear not gentle readers, i have not been complete idle when it comes to learning mathematics. A few years ago, i had a similar urge of trying to shore up knowledge, and bought a cute book called, "A very short introduction to mathematics."
Look at how cute!

Obviously, it is not a textbook, and it literally treats broad fields like cartesian geometry in paragraphs, and limits in sentences. But, reading this little bad boy i think i have started to understand some things that have long bugged me about math. I finally get the reason why 1.9999999 (repeating) is = to 2. And i think i understand the concept of pi a bit better, as well as the notion of irrational numbers.
I got a thrill at the idea that I was starting to understand a very abstract concept, in a real way. I am hoping that this project will continue to bring more of these thrills.
Monday, September 22, 2008
Over-Ambitious?
One obvious point was made to me earlier today. Using the GRE as a measure of what i have learned is enormously ambitious. I am not really re-learning what i forgot. True, i did take all of the subjects in one manner or another in college. But at least 1/3 to 1/2 of what they are testing, is in reference to junior and senior level courses. I have taken calculus, but i haven't taken number theory at all before. I may have taken physics, but our coverage of nuclear physics and statistical mechanics was at best perfunctory and more accurately a piffle's worth.
Should i scrap the project?
I tried to think of another means of measurement. Perhaps AP tests, or some other form that doesn't deal with giving money to the ETS.
But, I can't really think of another good measure.... so, i think what i may need to do is extend my timeline. The general concept would be to use a full year of studying before taking the two subject exams. I am stubborn though, so i am going to see where i am by February before abandoning my current timeline.
Wish me luck!
Sunday, September 21, 2008
Mathematics.. the language of God! Physics- God's Code!
After speaking with my father, I think I am going to pair Physics with Mathematics instead of literature. Pairing up math with physics will hopefully allow me to understand both better when i do study them. I am a bit dissappointed that I won't be starting up the literature section right away. Of course, i can always read stuff on my own as part of "relaxation", we'll see.
Approximately 66 questions. Questions are based on material learned during the undergraduate years. Approximately 50% of the questions are based on Calculus, 25% on Algebra, and 25% on Additional Topics. Algebra topics include:
I sadly am a bit behind, so I don't think I can start right in with calculus or advanced algebra.
So here is my plan for Math and Physics subjects that need to be covered.
The GRE tests cover for math:
- Elementary Algebra
- Linear Algebra
- Abstract Algebra and Number Theory
I sadly am a bit behind, so I don't think I can start right in with calculus or advanced algebra.
The first step will be Geometry and Trigonometry. This means getting some good high school text books on the subject. A neat idea would be to try and take some of the original greek texts, but i don't think that would be an efficient use of time. So, if anyone has suggestions for good trigonemtry or geometry textbooks, let me know.
After those, I will start with Calculus, Linear Algebra and then number theory etc. I do think i need to recover statistics as well, and will try and tie that in after Calculus.
The list and general order for my crash course in Mathematics.
Geometry
Trigonometry
Calculus
Statistics
Linear Algerbra
Number theory.
As for physics, here is what the GRE asks for
Main topics include:
Main topics include:
- Classical Mechanics – 20%
- Electromagnetism – 18%
- Optics and Wave Phenomena – 9%
- Thermodynamics and Statistical Mechanics – 10%
- Quantum Mechanics – 12%
- Atomic Physics – 10%
- Special Relativity – 6%
- Laboratory Methods – 6%
- Specialized Topics – 9%
I can think of very little reason to deviate from this list of topics. I don't know if I can really docus on laboratory methods, but i have had some past lab experience, so we'll see if i need to really review those materials.
What will be nice, is if i can pair my timing to be learning Calculus and Classical mechanics at the same time.
I will be relying on my dad to provide physics textbooks for me, but if anyone has any recommendations that would be cool.
Saturday, September 20, 2008
The Gameplan

One of the biggest ways to set myself up would be to go into this project with no accountability. I am not about to hire teachers, or have the ability to enter into a degree program with the purpose of "teach me everything i should have already learned. " So there are limited options here.
I think the easiest way to hold myself accountable would be to have some way to measure my progress by having a clear objective goal. That means testing. Just as with Lisa Simpson, I need some objective measure of my knowledge. In steps the Educational Testing Service. When I was about to graduate from college, I had absolutely no idea about what I was going to do. I was well on my way to getting a degree in Econ, but despite the fact that it sounds like a pragmatic degree, it quickly became apparent, that it was anything but pragmatic. No employer gave a shit about the fact that I could discuss utility curves and the concept of "stagflation." I had already freaked out in my 3rd year and ran away from a philosphy major for fear that I was going to be lost in abstraction, and would never be able to apply Kant's Critique of Judgement in a way that could support myself.
With graduation imminent, I thought my one way out of unemployment and a fate of knocking on doors trying to sell people on a pyramid scheme (an actual interview i had), grad school was going to be my way out. I registered for the GRE and took the basic test. I had no idea what area of graduate studies I was going to pursue, and I had an innate fear of following in my parents' footsteps, and so I hadn't taken any of the subject tests. Thankfully, I never had to use my score (I did well, but that wasn't the point as i couldn't apply for a graduate program in "verbal skills") as the tech boom was on, my learned ability to turn on a computer landed me a job post-college.
So what was the point of that digression? My plan of accountability and progress, is to sign up and re-take the GRE. And not just the Basic GRE which tests verbal skills, (which as a lawyer i hope mine haven't gone downhill), but also for a variety of subject tests. I whave decided to take the biology, biochem, chemistry, mathematics, physics and literature subject exams.
I don't plan on taking all of the subject tests at the same time, but in order to make this worthwhile, I am going to try and sign up for 2 tests at a time. I am also NOT going to study or use GRE specific materials. The entire point of this project is to actually teach myself these subjects and not just learn a subject for purposes of taking a test.
My Timeline
The exams are given out 3 times a year, April, October, and November. There is no way I can be ready for the exams by October or November, so I am going to plan for an April exam for my first 2 tests.
Afterwards, I am hoping I can get the next 2 in October or November. And then my one year anniversay will be for the final 2 subjects. This will hopefully mean that in 1 year and 7 months i will have learned 6 "elementary" subjects.
What am I leaving out
Computer Science and Psychology. Despite having taken a couple of comp sci courses, I never really learned computer science, and never took any psych classes, so I am leaving them out as subjects for now.
What am I going to tackle first?
I think I am going to focus on:
Mathematics & Literature
Chemistry and Physics
Biochemistry, Mol Biology and Biology
Needed Materials
Textbooks, texbooks, Textbooks and Books.
I have many of my college text books, but not all. I do work at a University, and i get a campus discount, though i can also easily look for used text books as well.
Progression Accountability
Luckily i have friends and family who teach and involved in many of these subject areas. I am going to try and get them on board, and ask them to periodically devise ways to make sure I am actually understanding what it is that i am learning.
The purpose of this blog
I hope to use this as a sort of experment logbook. I don't expect much of an audience, but I do want a means to record what it is that I am doing. I also hope that the mere existence of this blog will serve as a means of accountability.
My Goal
Right now, my plan is to try and score in the top 25%, or better than 75 percentile for all the subject areas. This may be too ambitious, but I would love to try.
What did I really learn in college, and what use is it?

After reading some of DFW's (David Foster Wallace) essays, I was reminded of my astonishment of his vast array of interests and passions. With some reflection, my astonishment quickly turned to a mixture of shame, curiosity, and inspiration. The inspiration hit me as I walked from my local coffee shop after chowing down on a piece of blueberry pie and a cup of white tea. Why don't I teach myself what I had supposedly learned in college? Why don't I relearn calculus, statistics, physics, chemistry, biology, and even literature? I have let my knowledge decay and die, existing only as footprints and wayward spirits in my mind.
How can i consider myself educated if I can't remember the definition of a derivative, or the laws of thermodynamics, how to reduce and oxidize basic chemical reactions, or even the significance of Thomas Mann, or yes, the Canterbury Tales and Aeschylus.
How I got Here
Lately, I had been feeling a bit lost on what I should do with my free time. I gave up a habit of playing WoW. Playing WoW started as all entertainment and distractions start, which was simply a way to unwind, and ultimately be passive. The allure of course, was that the game demanded attention, focus and participation. It was these demands that gave the game the illusion that playing it wasn't a passive way to spend one's time. There was social interaction, there were tasks that need to be completed, and of course, there were jolts of reward and reputation. Ultimately though, the singular reason i played was because it was a bridge from the time i came home, to the time i could force my head on the pillow and fall into an exhausted sleep. The bridge that occupied those hours of my days were certainly enjoyable, yet, when distraction is all that i could get out of it.. well then it is time to move on.
Why not Something Else?
There are two obvious questions. One, isn't my work fulfilling enough as it is? Why not use the time and energy more towards my work and career? Similarly, why don't I just use this time to develop or cultivate my personal relationships.
There are two obvious questions. One, isn't my work fulfilling enough as it is? Why not use the time and energy more towards my work and career? Similarly, why don't I just use this time to develop or cultivate my personal relationships.
First off, I do find my job fascinating, challenging, fun and exhililarating, and do so often. However, I had a father who, to my young eyes, seemed to throw his whole self into his work.He lived and breathed his research. If he was not at the lab, then he was merely at home asleep on his bed, or asleep in front of the television. I would give him books, but they were often unread, as he never seemed to have time for anything other than his research.
One seemingly very american cultural ideal is that we are what we do. I feared that ideal and lost of identity. In the end, I don't want my tombstone or legacy summed up by my work or my career.
As for my relationships.. this is a much harder question to answer. I have no doubt that if I were currently in a meaningful romantic relationship, or starting a family even, that i would never try this project. In many ways, the fear of distraction, can easily be abstracted into just loneliness. On the other hand, i hope i am wrong about my prediction that a relationship or a family would prevent me from fulfilling or even conceiving of this project. Just as i don't believe my idenity should not be summed up by my career, i also believe, that my identy shouldn't be wrapped up by my relationships with others. It would be my hope, that even with a girlfriend/wife/children, I would still see the need to shore up my basic education and knowledge.
The less obvious question, but equally valid, is why not try something more "normal." Don't most people in my situation go and try to learn a musical instrument? To travel? Learn to dance, or to take up a new hobby, perhaps building furniture, or scultping or bird watching? I suppose most would, and here is the thing.. I plan on trying all of, or in part the above. I want to learn a new language, would love to travel the world, and finally figure out if i can ever learn to create something meaningful.
And yet.. I don't feel prepared to do what "normal" people do in pursuit of cultivation. (I use that term not in reference to "high" art such as ballet or opera, but more of a fertile vision of cultivation as in agriculture, with our identities and beings as the black, rich soil.) One of the taglines we hear about education is that it helps us no matter what we want to do. We may not use geometic proofs, but learning the ability to go from Axioms to Rule teach us how to think clearly. We may not use literature outside of cocktail parties and attempts to impress women, but literary characters from Electra and Syndey Carlton gives us insights into ourselves. So it seems like a gaping maw, a missing building block of who I am, when I have let my knowledge to decay the way i have. And so, why not try and fix the situation, feed the soil of me, and ready it for new and interesting growths.
Subscribe to:
Posts (Atom)